Eletrônica

Assim podemos generalizar:
Por exemplo, com 3 dígitos hexadecimais podemos contar de 000 até FFF, que corresponde a faixa de 0 a 4095 em decimal, em um total de 16^3 = 4096 valores diferentes.
- Eletrônica Digital: Display De 7 Segmentos E Detecção De Erros
No tutorial anterior falei sobre código BCD, Gray e tabela ASCII, neste tutorial falarei sobre display de 7 segmentos e um pouco sobre as técnicas utilizadas na detecção de erros. Display de 7 Segmentos Hoje a tecnologia já está muito mais avançada,...
- Eletrônica Digital: Código Bcd, Gray E Ascii
No tutorial anterior falei sobre a conversão de um número de um sistema de numeração para o outro e também sobre faixa de contagem. Neste tutorial falarei sobre tabelas e códigos BCD, Gray e ASCII. Código BCD O código BCD foi criado para codificar...
- Eletrônica Digital: Conceitos Introdutórios
Este é o primeiro tutorial de eletrônica digital, tema este que foi escolhido por leitores do blog através de uma enquete. O tutorial será um pouco extenso pois este conteúdo nos irá introduzir os conceitos mais importantes sobre eletrônica digital....
- Diferenças Entre As Roms Da Cas 1986 E 1987
Verifiquei quais são as diferenças entre as duas versões da ROM da interface de drive CAS. As duas ROMs estão disponíveis no site do Eduardo Luccas. No shell do Linux, digitei o comando: cmp -l CAS-1986-DECOD.BIN CAS-1987-DECOD.BINPorém...
- Proteção De Programas Em Fitas: Constantes Numéricas
Eu já tive oportunidade, na série sobre adaptação de jogos para disquetes Beta 48, mencionar sobre proteção de programas BASIC contra listagem. Na ocasião, recomendei o uso do utilitário STK para poder carregar e listar tais programas. O que eu...
Eletrônica
Eletrônica Digital: Faixa de Contagem e Conversões
No tutorial anterior apresentei os sistemas de numeração decimal, octal, hexadecimal e binário. Neste tutorial trataremos da conversão de números de um sistema de numeração para o outro e também sobre faixa de contagem. Os métodos que empregarei são utilizados em diversos livros de eletrônica digital. É claro que pode existir outros métodos de conversão que eu desconheça e que talvez seja mais eficientes. Também existem softwares que fazem conversões e ajudam bastante.

Faixa de Contagem
Utilizando N bits, podemos contar 2^N (2 elevado a N) diferentes números em decimal, (de 0 até 2^N - 1). Por exemplo, com 4 bits (N=4), podemos contar de 0000 até 1111 em binário. Isso corresponde a um total de 16 números diferentes. A faixa de contagem é de 0 até 15. E há 2^4 números diferentes.
Generalizando podemos dizer o seguinte:
Usando N bits, podemos representar números decimais na faixa de 0 até 2^N-1, em um total de 2^N números diferentes.
Conversão Decimal Para Binário
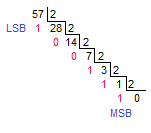
Para converter um número do sistema decimal para o sistema binário, basta utilizarmos o método da divisão por 2. Neste método, efetuamos a divisão do número decimal por 2 e só paramos assim que o quociente chegar em zero. A imagem a seguir ilustra esse procedimento.
Observe na imagem como foi feita a conversão do número 57 pelo método das divisões por 2. MSB significa "digito mais significativo" e LSB "digito menos significativo". Isso implica na forma como obtemos o número binário a partir do método. Logo, o número 57 em binário é 111001. Essa é a maneira mais simples de converter um número decimal para binário.
Mas como converter o número 5,4 de decimal para binário ? Para isso, primeiro convertemos 5 para binário pelo método das divisões, e o 0,4 é convertido pelo método da multiplicação por 2. Observe a imagem a seguir que ilustra essa etapa.
Observe na imagem os números grifados em vermelho, eles representaram os bits do número 0,4 já em binário. Veja também que em 1,6 não repetimos o 1 e multiplicamos 0,6 por 2 e não 1,6. Isso é feito para obtermos o digito em binário e segue da definição metódica de conversão. Esse método pode ser utilizado para converter números decimais fracionários em binário.
Observe também que temos uma dizima periódica em binário quando chega em 0,8. A partir daí podemos representar o número com os três pontos finais (...). Logo, o resultado da conversão de 5,4 decimal para binário é 101,01100... .
Se você encontrar uma conversão que resulte em uma dízima e não houver a especificação do número de bits máximos, aí a representação (a quantidade de bits) depois da dízima fica a nosso critério.
 |
| Figura 1 - Conversão decimal para binário. |
Mas como converter o número 5,4 de decimal para binário ? Para isso, primeiro convertemos 5 para binário pelo método das divisões, e o 0,4 é convertido pelo método da multiplicação por 2. Observe a imagem a seguir que ilustra essa etapa.
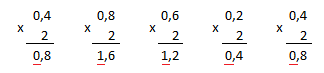 |
| Figura 2 - Conversão decimal para binário. |
Observe também que temos uma dizima periódica em binário quando chega em 0,8. A partir daí podemos representar o número com os três pontos finais (...). Logo, o resultado da conversão de 5,4 decimal para binário é 101,01100... .
Se você encontrar uma conversão que resulte em uma dízima e não houver a especificação do número de bits máximos, aí a representação (a quantidade de bits) depois da dízima fica a nosso critério.
Conversão Binário Para Decimal
Para converter um número escrito no sistema binário para o decimal, utilizamos o método da soma das potências de 2. É mais fácil entender o método observando o exemplo na imagem a seguir.
 |
| Figura 3 - Conversão binário para decimal. |
Pelo método observamos que devemos multiplicar cada bit (também chamado de peso) do número binário por um 2 elevado a alguma potência e somar tudo. Observe o último caso em que converti um número binário com vírgula (isso mesmo !). Podemos ter números binários com vírgula também. O método se aplica a qualquer número binário. Atente-se pois, o expoente zero vai para o primeiro bit à esquerda da vírgula e assim cresce sucessivamente. E o expoente -1 vai para o primeiro bit à direita da vírgula e assim decresce sucessivamente.
Conversão Hexadecimal Para Decimal
Para fazer a conversão de um número hexadecimal para o sistema decimal podemos utilizar o fato de que cada dígito em hexadecimal possui um peso que é uma potência de 16. Observe o exemplo a seguir em que o número 356 no sistema hexadecimal é convertido para decimal.
 |
| Figura 4 - Conversão hexadecimal para decimal. |
As conversões são bastante similares, porém devemos sempre fazê-las com muita atenção. Observe que o primeiro dígito é multiplicado por 16 elevado à 0, essa etapa é similar à conversão de binário para decimal porém com peso 16.
Conversão de Decimal Para Hexadecimal
Assim como na conversão de decimal para binário utilizamos o método das divisões sucessivas, aqui também não será diferente. Utilizaremos o método das divisões sucessivas porém, agora dividindo por 16. Observe no exemplo a seguir como foi feito a conversão do número 423 de decimal para hexadecimal.
 |
| Figura 5 - Conversão decimal para hexadecimal. |
Uma observação muito importante é que: qualquer resto de divisão que seja maior do que 9, é representado pelas letras (A até F) correspondentes ao número em hexadecimal.
No exemplo da figura acima obtemos o número 1107 em hexadecimal, porém temos o número 10 como resto, então pela definição a conversão correta é 1A7 em hexadecimal. Não é muito complexo realizar as conversões, só exige atenção e que as regras sejam seguidas rigorosamente.
Conversão Hexadecimal Para Binário
Para fazer a conversão de um número em hexadecimal para o seu equivalente no sistema binário, é necessário entender que um número em hexadecimal é representado por 4 bits, ou seja, cada dígito hexadecimal é constituído de 4 bits em binário. Por exemplo, converter o número 9F2 de hexadecimal para binário.
 |
| Figura 6 - Conversão hexadecimal para binário. |
Observe que cada dígito hexadecimal possui os 4 bits.
Conversão Binário Para Hexadecimal
A conversão de um número binário para seu equivalente no sistema hexadecimal é feita de forma relativamente simples. Basta lembrar que um dígito em hexadecimal é composto por 4 bits em binário. Logo, para fazer a conversão basta agrupar o número binário em grupos de 4 bits. Observe a imagem a seguir para compreender melhor como é feito este processo.
 |
| Figura 7 - Conversão binário para hexadecimal. |
Outra observação muito importante está na forma de como é feito esse agrupamento. Inicia-se o agrupamento da direita para a esquerda e quando falta bits, completamos acrescentando zeros à esquerda. O exemplo foi proposital para mostrar o processo de completar os zeros à esquerda.
Faixa de Contagem em Hexadecimal
Quando contamos em hexadecimal, cada dígito pode ser incrementado (acrescido de 1) de 0 até F (15 em decimal). Quando o dígito de uma posição chegar no valor F, este volta para 0 e o dígito da próxima posição é incrementado. Como exemplo, tome a seguinte contagem em hexadecimal.
 |
| Figura 8 - Contagem em hexadecimal. |
Observe no exemplo a mudança de 9 para A e de F para 0, e o incremento no dígito seguinte.
Assim podemos generalizar:
Com N dígitos hexadecimais podemos contar de 0 até 16^N - 1, em um total de 16^N valores diferentes.
Por exemplo, com 3 dígitos hexadecimais podemos contar de 000 até FFF, que corresponde a faixa de 0 a 4095 em decimal, em um total de 16^3 = 4096 valores diferentes.
Conversão Octal Para Decimal
Assim como no sistema binário e hexadecimal, a conversão de um número octal para decimal é feita de forma similar aplicando o mesmo método. Bastando aplicar a soma dos pesos de potência de 8. Por exemplo converter o número 372 de octal para decimal.
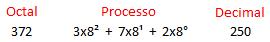 |
| Figura 9 - Conversão octal para decimal. |
Observe a grande similaridade entre a conversão de um sistema para o outro.
Conversão Decimal Para Octal
Converter um número decimal para octal basta aplicarmos o método das divisões sucessivas por 8. Observe na imagem a seguir como é o procedimento para fazer a conversão de 1024 decimal para octal.
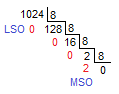 |
| Figura 10 - Conversão decimal para octal. |
Feito as divisões sucessivas por 8, basta agrupar o resultado, que segundo o método dá 2000 no sistema octal.
Conversão Octal Para Binário
Para converter um número do sistema octal para o binário o procedimento é relativamente simples, basta converter cada dígito octal para binário de 3 bits. Tome o exemplo a seguir em que o número 73 em octal é convertido para binário.
 |
| Figura 11 - Conversão octal para binário. |
Conversão Binário Para Octal
A conversão de um número binário para seu equivalente no sistema octal também não é uma tarefa muito complexa. Basta agrupar o número binário em grupos de 3 bits, iniciando da direita para esquerda. E completar com zeros à esquerda caso seja necessário. Observe como isso é feito no exemplo a seguir.
 |
| Figura 12 - Conversão binário para octal. |
Observe que a conversão de binário para octal se assemelha à conversão de binário pra hexadecimal. Olhe como realizar as conversões são simples, porém exigem muita atenção.
Este tutorial termina por aqui, ficou um pouco extenso mas, são parte do processo de aprendizagem.
Espero que tenham gostado. Qualquer dúvida, sugestão ou crítica deixe seu comentário aqui ou na nossa fan page, aliás curta lá para você ficar mais próximo das novidades e mantermos maior contato.
Para o próximo tutorial vamos ver um pouco sobre alguns códigos (BCD, Gray e outros).
Até o próximo !
loading...
- Eletrônica Digital: Display De 7 Segmentos E Detecção De Erros
No tutorial anterior falei sobre código BCD, Gray e tabela ASCII, neste tutorial falarei sobre display de 7 segmentos e um pouco sobre as técnicas utilizadas na detecção de erros. Display de 7 Segmentos Hoje a tecnologia já está muito mais avançada,...
- Eletrônica Digital: Código Bcd, Gray E Ascii
No tutorial anterior falei sobre a conversão de um número de um sistema de numeração para o outro e também sobre faixa de contagem. Neste tutorial falarei sobre tabelas e códigos BCD, Gray e ASCII. Código BCD O código BCD foi criado para codificar...
- Eletrônica Digital: Conceitos Introdutórios
Este é o primeiro tutorial de eletrônica digital, tema este que foi escolhido por leitores do blog através de uma enquete. O tutorial será um pouco extenso pois este conteúdo nos irá introduzir os conceitos mais importantes sobre eletrônica digital....
- Diferenças Entre As Roms Da Cas 1986 E 1987
Verifiquei quais são as diferenças entre as duas versões da ROM da interface de drive CAS. As duas ROMs estão disponíveis no site do Eduardo Luccas. No shell do Linux, digitei o comando: cmp -l CAS-1986-DECOD.BIN CAS-1987-DECOD.BINPorém...
- Proteção De Programas Em Fitas: Constantes Numéricas
Eu já tive oportunidade, na série sobre adaptação de jogos para disquetes Beta 48, mencionar sobre proteção de programas BASIC contra listagem. Na ocasião, recomendei o uso do utilitário STK para poder carregar e listar tais programas. O que eu...
